本文共 5334 字,大约阅读时间需要 17 分钟。
文章目录
用户账号和组账号概述
Linux基于用户身份对资源访问进行控制
用户账号
-
超级用户:root 用户是 Linux 操作系统中默认的超级用户账号,对本主机拥有最高的权限。系统中超级用户是唯一的。
-
普通用户:由root用户或其他管理员用户创建,拥有的权限会受到限制,一般只在用户自己的宿主目录中拥有完整权限。
-
程序用户:在安装Linux操作系统及部分应用程序时,会添加一些特定的低权限用户账号,这些用户一般不允许登录到系统,仅用于维持系统或某个程序的正常运行,如 bin、daemon、ftp、mail 等。
组账号
-
基本组(私有组):基本组账号只有一个,一般为创建用户时指定的组。
在/etc/passwd文件中第4字段记录的即为该用户的基本组 GID 号。 -
附加组(公共组):用户除了基本组以外,额外添加指定的组。
UID和GID
- UID:用户标识号
- GID:组标识号
- root 用户账号的 UID和GID 号为固定值 0
- 程序用户账号的 UID和GID 号默认为 1~499
- 普通用户的 UID和GID 号默认为500~60000
用户账号文件
用户账号文件/etc/passwd
保存用户名称、宿主目录、登陆shell等基本信息
基于系统运行和管理需要,所有用户都可以访问/etc/passwd文件中的内容,但是只有root用户才能进行更改。 在早期的UNIX操作系统中,用户帐号的密码信息是保存在passwd文件中的,不法用户可以很容易的获取密码字串并进行暴力破解,因此存在一定的安全隐患。后来经改进后,将密码转存入专门的shadow文件中,而passwd文件中仅保留密码占位符“x”。 每一行对应一个用户的账号记录
root:x:0:0:root:/root:/bin/bash字段1:用户帐号的名称 (root)字段2:用户密码占位符“x”(x)字段3:用户帐号的UID号(0)字段4:所属基本组帐号的GID号(0)字段5:用户全名(root)字段6:宿主目录(/root)字段7:登录Shell信息(/bin/bash为可登陆系统,/sbin/nologin和/bin/false为禁止用户登陆系统;)
用户账号文件/etc/shadow
保存用户的密码、账号有效期等信息
默认只有 root 用户能够读取 /etc/shadow 文件中的内容,且不允许直接编辑该文件中的内容。 每一行对应一个用户的密码记录
root:$6$VyOUGqOC$v5HlLM1wagZC/FwGfnrtJFnlT:18445:0:99999:7:::字段1:用户帐号的名称(root)字段2:使用MD5加密的密码字串信息,当为“*”或“!!”时表示此用户不能登录到系统。若该字段内容为空,则该用户无须密码即可登录系统($6$VyOUGqOC$v5HlLM1wagZC/FwGfnrtJFnlT)字段3:上次修改密码的时间,表示从1970年01月01日算起到最近一次修改密码时间隔的天数(18445)字段4:密码的最短有效天数,自本次修改密码后,必须至少经过该天数才能再次修改密码。默认值为0,表示不进行限制(0)字段5:密码的最长有效天数,自本次修改密码后,经过该天数以后必须再次修改密码。默认值为99999,表示 不进行限制(99999)字段6:提前多少天警告用户密码将过期,默认值为7(7)字段7:在密码过期之后多少天禁用此用户(空)字段8:帐号失效时间,此字段指定了用户作废的天数(从1970年01月01日起计算),默认值为空,表示账号永久可用。(空)字段9:保留字段(未使用)(空)
添加用户账号 useradd 或者 adduser
在/etc/passwd 文件和/etc/shadow 文件的末尾增加该用户账号的记录。
若未明确指定用户的宿主目录,则在/home目录下自动创建与该用户账号同名的宿主目录,并在该目录中建立用户的各种初始配置文件。 若没有明确指定用户所属的组,则自动创建与该用户账号同名的基本组账号,组账号的记录信息将保存到/etc/group 和/etc/gshadow 文件中。 在使用 useradd或者adduser添加一个用户的时候,是不能进行任何操作的,因为没有将这个用户进行激活。只有给这个用户配置一个密码之后才能被激活,然后才能进行操作。useradd 命令
useradd [选项] 用户名
常用选项:
-u:指定用户的 UID 号,要求该 UID 号码未被其他用户使用。-d:指定用户的宿主目录位置(当与-M 一起使用时,不生效)。-e:指定用户的账户失效时间,可使用 YYYY-MM-DD 的日期格式。-g:指定用户的基本组名(或使用 GID 号),对应的组名必须已存在。-G:指定用户的附加组名(或使用 GID 号),对应的组名必须已存在。-M:不建立宿主目录。-s:指定用户的登录 Shell,(比如/bin/bash为可登陆系统,/sbin/nologin和/bin/false为禁止用户登陆系统)。


为用户账号设置密码 passwd
root用户可以指定用户名作为参数,对指定账号的密码进行管理。
普通用户却只能执行单独的“passwd”命令修改自己的密码。命令格式:passwd [选项] 用户名
常用选项:
-d:清空指定用户的密码,仅使用用户名即可登录系统。-l:锁定用户账户,锁定的用户账号将无法再登录系统。-S:查看用户账户的状态(是否被锁定)。-u:解锁用户账户。(-u解锁时,如果没有密码会提示,需要使用-f强制解锁)
设置shengmo密码:
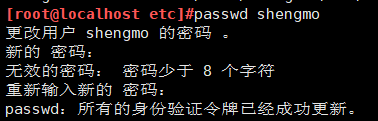

锁定shengmo的密码并查看是否已锁定
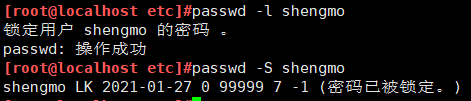
锁定后登录界面账号不见了,就算输入账号密码也无法登录
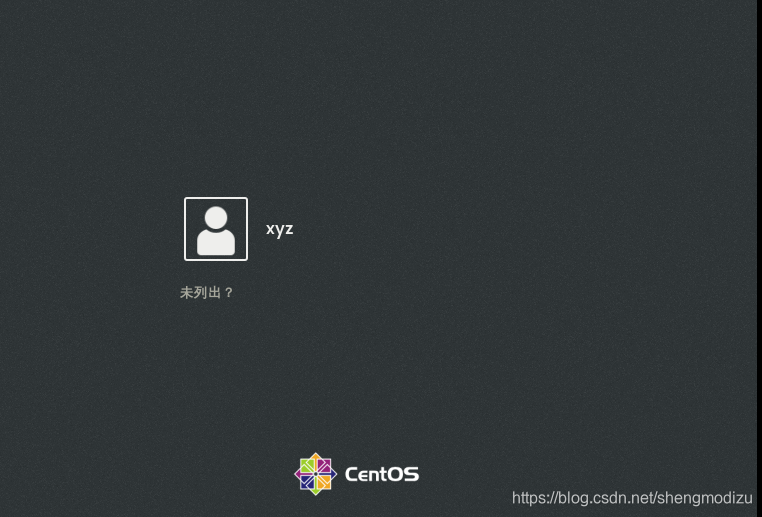
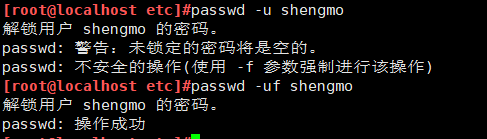
解锁后,登录界面上账号也回来了

修改用户账号属性 usermod
命令格式:usermod [选项] 用户名
常用选项:
-u:修改用户的 UID 号。-d:修改用户的宿主目录位置。-e:修改用户的账户失效时间,可使用 YYYY-MM-DD 的日期格式。-g:修改用户的基本组名(或使用 GID 号)。-G:修改用户的附加组名(或使用 GID 号)。-s:指定用户的登录 Shell。-l:更改用户账号的登录名称。-L:锁定用户账户。-U:解锁用户账户。
删除用户账号 userdel
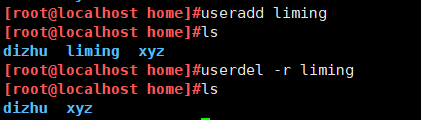
命令格式:userdel [-r] 用户名
添加“-r”选项时可以将该用户的宿主目录一并删除
用户账号的初始配置文件
文件来源
- useradd 命令添加一个新的用户账号后在该用户的宿主目录中建立一些初始配置文件。
- 这些文件来自于账号模板目录/etc/skell,基本上都是隐藏文件。
用户宿主目录下的初始配置文件只对当前用户有效
~/.bash_profile #此文件中的命令将在该用户每次登录时被执行,它会设置一些环境变量,并且会调用该用户的~/.bashrc文件~/.bashrc #此文件中的命令会在每次打开新的bash shell时(也包括登录系统)被执行,并且会调用/etc/bashrc文件~/.bash_logout #此文件中的命令将在用户每次退出登录或退出bash shell时执行
全局配置文件对所有用户有效
/etc/profile #这个文件是为系统全局变量配置文件,可通过重启系统或者执行source /etc/profile 命令使profile文件被读取/etc/profile.d #这个文件实际上是/etc/profile的子目录,存放的是一些应用程序所需的启动脚本/etc/bashrc #每一个运行bash shell的用户都会执行此文件,可通过执行bash 命令打开一个新的bash shell时,使 bashrc文件被读取
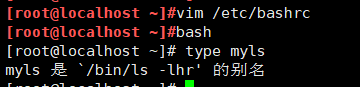
更改全局配置,使每个用户下的/bin/ls -lh命令都改成myls
vim /etc/bashrcalias myls='/bin/ls -lhr'bash 切换到bash的子进程中type myls exit 退出子进程
PATH变量用于设置可执行程序的默认搜索路径
PATH 生效的原理: 每次启动系统的时候会初始化命令,会执行/etc/profile和~/.bash_profile。/etc/profile会将路径/usr/local/bin 、/usr/bin、/usr/local/sbin 、/usr/sbin 追加到PATH中去。然后调用 /etc/profile.d 目录下的脚本。组账号文件
/etc/group:保存组帐号基本信息/etc/gshadow:保存组帐号的密码信息[root@promote home]#grep "postfix" /etc/groupmail:x:89:postfixpostfix:x:12字段1:组帐号的名称字段2:占位符“x”字段3:组账号的GID号字段4:组账号包含的用户成员(一般不包括基本组对应的用户帐号),多个成员之间以逗号“,”分隔

添加删除组账号 groupadd
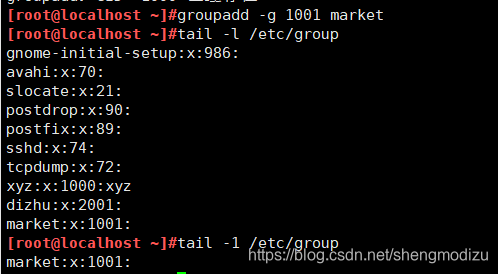
添加组账号
命令格式:groupadd [-g GID] 组账号名示例:groupadd -g 2000 ceshi2 添加一个组账号名为ceshi2,GID号为2000的组账号 tail -1 /etc/group 查看此文档的最后一行,一般最后一行就是刚添加的
添加删除组成员 gpasswd
设置组账号密码(极少用)、添加/删除组成员
命令格式:gpasswd [选项] 组账号名
常用选项:
-a:向组内添加一个用户-d:从组内删除一个用户成员-M:定义组成员列表,以逗号分隔
建立lisan,将lisan加入dizhu的组中,查询lisan所属的组
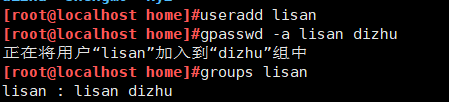
删除lisan
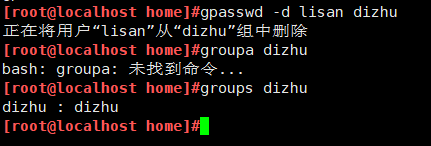
查询账号信息
查询用户所属的组 groups
groups [用户名]
查询用户身份标识 id
id [用户名]
查询账号信息
finger命令 ——查询用户账号的登陆属性
注:需要先进行安装finger软件包yum install -y finger 安装finger(版本可能不一样,可以直接Tab补齐)finger [用户名]
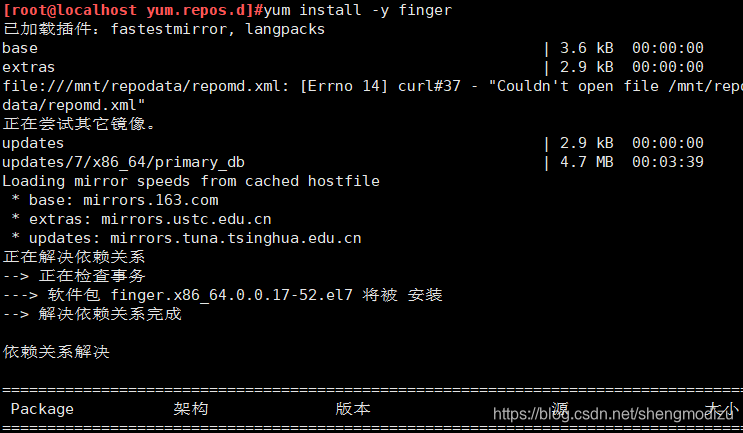
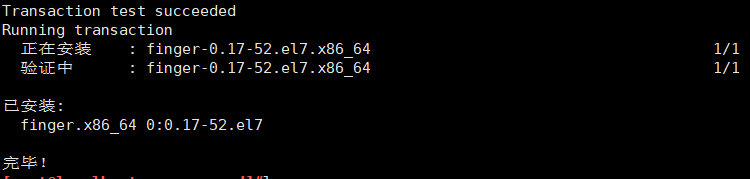
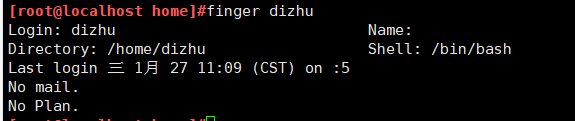
查询已登录到主机的用户信息
w 、who、users命令

- 通常使用tty来简称各种类型的终端设备,Centos7系统,tty1表示图形界面,tty2-tty6表示文字界面,可以用Ctrl+Alt+F1-F6切换。
- 按Ctrl+Alt+F2登陆,执行w 命令,使用的终端就是tty2
- pts说明是用远程工具连接的,比如xshell,后面的数字代表登录的时间顺序,越小证明登录的越早
文件/目录的权限和归属
访问权限:
- 读取r:允许查看文件内容、显示目录列表
- 写入w:允许修改文件内容,允许在目录中新建、移动、删除文件或子目录
- 可执行x:允许运行程序、切换目录
归属(所有权)
- 属主:拥有该文件或目录的用户帐号
- 属组:拥有该文件或目录的组帐号
查看文件/目录的权限和归属
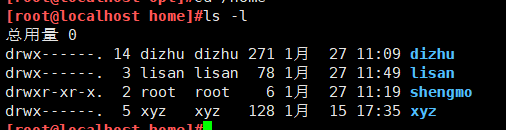
drwx------. 14 dizhu dizhu 271 1月 27 11:09 dizhu文件类型和权限 属主 属组对照下面的图可以看出这个文件的权限为:700


设置目录和文件的权限 chmod
1. chmod [ugoa…][+-=][rwx] 文件或目录“ugoa”表示该权限设置所针对的用户类别。“u”代表文件属主,“g”代表文件属组内的用户,“o”代表其他任何用户,“a”代表所有用户(缺省时为a)。“+-=”表示设置权限的操作动作。“+”代表增加相应权限,“-”代表减少相应权限,“=”代表仅设置对应的权限。“rwx”是权限的字符组合形式,也可以拆分使用,如“r”“rx”等。2. chmod nnn 文件或目录“nnn”表示三位八进制数-R:递归修改指定目录下所有子目录及文件的权限
设置目录和文件的归属 chown
chown 属主 文件或目录chown :属组 文件或目录chgrp 属组 文件或目录chown 属主:属组 文件或目录chown 属主.属组 文件或目录-R:递归修改指定目录下所有子目录及文件的归属
设置目录和文件的默认权限 umask
作用:
- 指定目前用户在新建文件或目录时的权限默认值
- 新建的文件或者目录的权限为默认最大权限减去umake(普通文件的最大默认权限为6,目录的最大默认权限为7)
umask设置:umask 022
umask查看:umask 示例:- 将umask设为000,新建目录或者文件,查看权限
- 将umask设为022,新建目录或者文件,再查看权限
转载地址:http://bpis.baihongyu.com/